Some 20th Century Physics, a lecture by Ricardo Nirenberg. Fall 1996, the University at Albany, Project Renaissance.
Last time, talking about genetics, I left you with a question about the meaning of "same" and "different." Today we'll take a very brief look at 20th century physics, and discuss how Einstein made sense of the results of various experiments and of the terms in certain formulas by analyzing what we mean when we say that two events happen "at the same time," or "simultaneously." This analysis is contained in the Special Theory of Relativity, published in 1905.
First, let us define what is meant by Relativity in physics. It is a principle that goes back to Galileo and Newton and, contrary to popular opinion, has nothing to do with saying that "everything is relative," or "it all depends on your perspective." Galileo's and Newton's Principle of Relativity says this: if we are in some vehicle, say a car or a space rocket, which travels in a straight line with uniform velocity, there is no way we can detect that we are moving by performing mechanical experiments. Even if we look out, we won't be able to say whether it's us or the landscape that's moving in the opposite direction. Of course, if the velocity is not uniform, if there's non-zero acceleration, we can detect we're moving, for example by feeling the force that pushes us against the seat when we step on the gas, or pushes us forward when we step on the brakes. That force can be computed by using Newton's second law. In mathematical language, the Relativity Principle can be expressed as follows: suppose we are traveling in a car with uniform velocity u in the direction of the positive x-axis; there's a difference between the x-coordinate of any point as seen from a fixed point in the ground (call it x) and as seen from our car (call it x'), and that difference is given by x' = x - ut, where t is the time elapsed. For example, if we are traveling at 60 m/h on 87South, the distance between NY City and Albany is 157 miles, but between our car and NY City it will be 157 miles minus 60m/h times the time since we started in Albany, in hours. Now, when we replace this new x' instead of the old x in Newton's laws of motion, nothing changes, you cannot notice the difference, the reason being that Newton's laws contain the second derivative of the position function (the acceleration) but no first derivatives, and when we take the second derivative, the term u times t disappears. This is the classical Principle of Relativity (long before Einstein!)
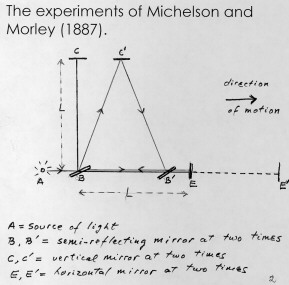
But what about electromagnetic radiation, in particular light, of which we talked in the previous lecture on Matter, Heat and Light? Perhaps some experiment might be conducted inside our car or rocket ship, not a mechanical one but one involving light or perhaps radio waves, which would detect our motion in a straight line with uniform speed? As I mentioned before, the British physicist Maxwell gave a set of equations governing the propagation of electromagnetic radiation; the finished form was published in 1873. These equations involve math that's too hard for us, so I will not show them to you, but I will remark that they involve first derivatives with respect to time, so that if we change the coordinate x (referred to a fixed point) by the coordinate x' = x - ut (the way we see things from our car), the equations will change, there will appear an extra quantity, the velocity u. This motivated physicists to try to find out a way to detect this uniform velocity u by means of experiments with light. The most famous of these experiments is the one by Michelson and Morley, done in 1887. It involves light interference, which I mentioned in the previous lecture: we have a light source, and the light hits a semi-reflecting mirror, so that part of the light is reflected and part of it goes through; the two beams of light then follow two different paths, each hits a mirror and is reflected back onto a screen. Because of the wave nature of light, if the paths of the two beams differ in length by certain amounts, there is interference, that is, the screen is dark: the two beams annihilate each other. For other differences in length, the two beams reinforce each other and the screen is brightest. Michelson's and Morley's idea was to take this apparatus and impart on it a uniform velocity in a given direction (they simply used the velocity of our planet around its orbit). The distance between the semireflecting mirror and the two mirrors here is the same, say L, but the beam moving in the same direction as the motion of the apparatus will have to travel (from semireflecting mirror to mirror and back) a different distance than the other beam, which moves in a perpendicular direction. For a diagram of this experiment, see Feynman's book, chapter 15, page 3. Indeed, once we measure those distances (which involves no more than simple geometry—try it!), it turns out that the time taken by the beam #1, the one going in the same direction as the apparatus, to arrive at the mirror and back to the semireflecting mirror is: 2L/c divided by 1 - u2/c2, where L is the distance between the semireflecting mirror and either of the two mirrors, c is the speed of light (in the vacuum), roughly 186,000 miles per second, and u is the speed of the apparatus itself (in this experiment, the same as that of the earth in its orbit, which is roughly 18 miles per second).
In a similar way, we compute the time taken by beam #2, the one perpendicular to the motion of the apparatus, to go from semireflecting mirror to mirror and back, and it is equal to: 2L/c divided by the square root of 1 - u2/c2. So the two times are different! Notice that the time for beam #2 contains the square root in the denominator, which is what makes the difference. What's the significance of this? If the two times are different, we should be able to measure exactly this difference by looking at how the two beams interfere with each other (the interference pattern), and once we know this difference in the times, simple algebra will tell us what's the velocity u of the apparatus. This would mean, then, that we could tell that the apparatus is moving with uniform velocity u by carrying out an experiment with light, which in turn would tell us that the Relativity Principle does NOT hold for light (and other electromagnetic radiation).
Well, the experiment was carried out again and again, and there were NO interference effects. In other words, the times taken by the two beams showed NO difference. How could this be? All kinds of explanations were offered. The above computation of the times is based on the assumption that the speed of light c is independent of the velocity of the source (the light bulb, say), and this assumption is a consequence of Maxwell's equations. Some people proposed that perhaps Maxwell's equations were wrong, and the speed of light should perhaps depend on the velocity of the source. But this suggestion led to results contrary to experience. Finally, the Dutch physicist H. Lorenz suggested the following outrageous solution: material objects shrink when they move! More specifically, if a yardstick, say, moves, it will experience a shortening in the direction of the motion, so that if it is moving parallel to itself it will measure less than a yard. Moreover, Lorenz said, this shortening happens by a factor equal to the square root of 1 - u2/c2, where, as before, u is the velocity of the thing (the yardstick) and c is the speed of light. With this shortening factor, the times taken by the two beams in the Michelson-Morley experiment turn out to be the same. But of course, people protested: Lorenz seemed to have proposed this shortening factor precisely to make the two times equal, but who could take it seriously, that things shrink when they move? As it turns out, Lorenz was right, but it was Einstein who first explained (in 1905) why this shrinking or shortening is observed and connected it to many other physical phenomena.
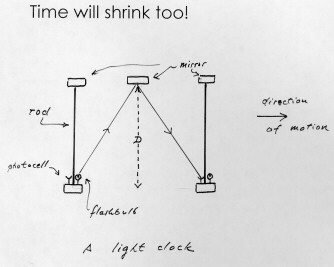
Remarkably, motion makes time shrink too! Let's see why this happens. First of all, after the failure of Michelson-Morley's and other experiments to produce a positive result, Henri Poincaré and Albert Einstein proposed that this failure must be due to a law of nature: our total inability to detect by any physical experiment, even those involving electromagnetic radiation like light, whether or not we are moving in a straight line with uniform velocity: this is, again, the Principle of Relativity. Now, let's imagine a simple clock: there's a source of light A and attached to it by a rod of length D, a mirror B where the light is reflected back to A; at A we have a photoelectric cell or some other means of detecting the beam of light when it hits it, so each time that happens it is registered. By counting how many times the light goes back and forth, we can measure the time elapsed. (See the diagram in Feynman's book, chapter 15, p.6) If we place this "light clock" inside a space ship going in a straight line with speed u, so that the clock rod is perpendicular to the direction of motion, something interesting happens: an observer inside the space ship will see the light in the clock going straight up and down, up and down, marking time; but suppose we observe this from the earth (imagine the space ship is transparent): we will not see the light going up and down always through the same path, rather we'll see it going through longer, diagonal paths, because the whole thing is moving with velocity u. Again, we can use Pythagoras' theorem and some simple algebra to figure out the difference between the times as perceived by the two observers. For the one inside the space ship, light takes t = 2D/c seconds to go back and forth, since it must travel along the rod twice, and c is the velocity of light. But for the observer on earth, if we call t' the time it takes from his point of view for the light beam to go back and forth, since during that time the point A, which is, remember, inside the space ship, has moved a distance ut', the distance light must traverse (by Pythagoras' theorem) is 2 times the square root of D2 + u2t'2/4. Therefore, the time t' will be equal to this distance divided by the speed of light, c, and we get that t' = 2/c times the square root of D2 + u2t'2/4. Now using algebra to solve for t' (we'll do this on the board during the lecture, but you're encouraged to try it yourself), we obtain finally that t' is equal to the old t (the time as viewed by the guy inside the space ship) divided by the square root of 1 - u2/c2. Do you think Pythagoras ever imagined that his theorem and his square roots would yield such strange results? For what we get from here is that time t' is larger than t, or in other words, from the point of view of the observer on earth, the time inside the space ship runs slower! This is because t' is obtained from t by dividing by a number smaller than 1: notice that 1 - u2/c2 is always smaller than 1, since we are subtracting a positive quantity from 1. But we must also observe that for that number to be noticeably different from 1, u has to be quite close to c, that is, the space ship has to go pretty fast. At the speeds u we are used to, the quotient u2/c2 will be so small that we won't be able to notice any difference in the two times.
One could object that this particular clock behaves in this crazy way, but perhaps some other type of clock like my Timex Ironman watch won't. Here the Principle of Relativity comes to our help: if you, inside the space ship, could detect a difference in the times marked by the light clock and your Timex watch, you would be able to tell you're moving, but we decided this is impossible. So all clocks will be slowed down by the indicated amount, not just the light clock. One could further object that all of this is speculative (literally, for we are using mirrors! Please look "speculative" up in the dictionary to get the joke) and that perhaps the Principle of Relativity is not universally true. But many experiments have been conducted, indicating that these results are in very precise agreement with observation. See, for example, the experiment with muons (very ephemeral particles) in Feynman, ch. 15, p. 7.
Don't come out of the space ship yet. While we're there, let us see how Einstein criticized the notion of simultaneous events, that is, the notion that two events happen at the SAME instant of time. How would you decide if two clocks (whether light clocks or Timex doesn't matter) are in synchrony? Say you are still inside the space ship: one way of setting the two clocks in synchrony is to place them at opposite ends of your ship, mark the middle point in between, and send two beams of light from that middle point in the direction of the two clocks; when the beams arrive, the clocks will start ticking--obviously at the same time, since the speed of light is constant, c, and it has to travel equal distances. But to the observer on earth, the two arrivals are not simultaneous, because the ship is moving with speed u in the same direction as the beams of light, so the beam going towards the rear of your ship travels a shorter distance than the beam going toward the front, and they do not arrive at the same time. Thus, you see, the two events which are simultaneous for the person inside the ship are not simultaneous for the person on earth. The very notion of simultaneous events is problematic, and it depends on our system of reference. Here's another example of how science and pure thought problematizes the notion of sameness (in this case, the notion of "at the same time"): we talked about that before, and we will return to it later, when we talk about quantum behavior.
To finish with this rapid review of Einstein's Special Relativity (there's a General Theory of Relativity, having to do with gravitation, but we will not touch on it), let's add that to make things cohere, to maintain such basic laws as conservation of energy, once we know that distances and time are changed when things move at high velocities, we must have the mass of physical objects change too. Indeed, when an object is moving with speed u, its mass m (let's say it is mo when it is at rest) increases by the same factor as we saw before: 1 divided by the square root of 1 - u2/c2. So even if you have a very light particle like an electron, if it is moving with a speed near that of light, it will be very massive, which means, according to Newton's second law, that you will need a pretty strong force to deflect it. Again, this has been observed and measured many times.
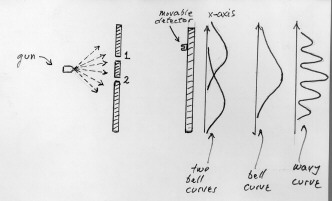
Let us now look at a different kind of experiment exhibiting what's called "quantum behavior." These experiments are more fully described in chapter 37 of Feynman's book, which you should read. To start with, imagine you have a wall with two holes or slits in it, which we'll number 1 and 2. On one side of the wall we'll place a gun which shoots tiny bullets at random in all directions (or at least in a wide angle of directions): these bullets can go through holes 1 and 2; on the other side of the wall we'll place an absorbing board, and we'll have a detector which can run all along this board and count the number of bullets which hit it per unit time. Of course, the bullets counted will be the ones that go through the wall by either hole 1 or hole 2 and end up hitting the detector at whatever position it happens to be. This apparatus allows us to graph the frequency with which bullets reach each point x of the absorbing board. If we cover hole 2 and let bullets go only through hole 1, the frequency of hits on the absorbing board follows a bell-shaped curve with its maximum at the point x1 where the line joining the gun and hole 1 intersects the board; far away from that point bullets hit but seldom. Similarly, if we cover hole 1 and let bullets through hole 2, the frequency of hits follows a bell curve with its max at the point x2 where the line joining gun and hole 2 intersects the board. What happens if we now let bullets go through both hole 1 and hole 2? As is to be expected, the frequency follows a bell curve that's essentially the sum of the previous two bell curves, with its maximum now at the midpoint: (x1 + x2)/2. In other words, the effect of having both holes open is the sum of the effects of having each of the two holes open.
We will now change the experiment as follows: we will submerge the whole apparatus in water, and instead of the gun, we'll install a device which produces ripples (waves) in the water; instead of the number of bullets the detector, then, will detect the amplitude of the ripples; to be specific, the square of the height of the ripples so that we won't have cancellations between a high crest and a low one. When a wave reaches a hole, it will produce new waves which will proceed toward the absorbing board in the back. When we repeat the previous experiments, first closing hole 1 then hole 2, then leaving both open, we find a different result: when one of the holes is closed, we get bell curves like before, but when we open both, we do not get the sum of the effects. The reason is that there is interference: high crests may cancel low ones, just as in the case of light interference which we discussed in a previous lecture. So the resulting curve will be rippled, with ups and downs. Whenever we deal with waves, we must expect interference phenomena.
Let us now change the experiment again: no water anymore, and instead of the original gun we'll install an electron gun, a device that shoots electrons instead of bullets. We proceed as before, closing hole 1 then hole 2, then leaving both open. The final curve shows interference, just as in the case of ripples or waves, even though electrons behave like bullets in another respect, namely that they arrive in discrete numbers (1,2,3, etc.), whereas the amplitude of a wave can be any number in between (a continuous quantity). So we have the surprising result that electrons behave partly like waves, partly like particles or tiny bullets! But reality is even more surprising. If we now place a device between the holes and the back board to let us see which hole each electron goes through, lo and behold, the final pattern will show no interference at all: the electrons stop behaving like waves and now behave purely like bullets! So the final result, whether there's interference or not, depends on whether or not we're observing which hole was chosen by the electron. This is what's called quantum behavior, and as you can read in Feynman's book, a consequence of this type of experiment is Heisenberg's Uncertainty Principle: we cannot measure both the position and the momentum of a body with absolute precision. In fact, the product of the errors made in those two measurements must be larger than a universal constant called Planck's constant.
A natural question is: if electrons behave like both particle and wave, how can we interpret, in the case of electrons, the amplitude of the wave, the quantity we were measuring in the experiment with water? It is usually interpreted as the probability of finding the electron at a given position or in a given state. In Quantum Mechanics, probability theory plays a fundamental role: physics becomes less deterministic than it used to be in the 18th and 19th centuries, and instead of dealing with precise measurements of location and momentum, for example, it deals with probability distributions. But this should be enough as introduction.
Required Reading:
Chapters 15 and 37 of Feynman's book.