Math 461: Topology
Math 461: Topology
Marco Varisco,
[email protected]
[how to email a professor],
math.binghamton.edu/marco/topology/
Office:
LN-2232,
Office Hours: MW 3:30–5:00 or by appointment.
MWF 2:20–3:20 in LN-1406
and R 1:15–2:40 in LN-1408.
N.B.: The Thursday meeting is not a discussion
session.
You are expected to attend all class meetings. The maximum number of absences permitted to receive credit for this course is 5 (five). Excessive tardiness may count as absence. [University Bulletin]
Math 304: Linear Algebra, and Math 323: Calculus III, and Math 330: Intro to Higher Math; or consent of Department. [University Bulletin]
“Study of topological spaces. Metric spaces, separation properties, connectivity, compactness.” [University Bulletin]
James Munkres, Topology, Second Edition, Prentice Hall, 2000.
Of course, you are expected to obey the Student Academic Honesty Code.
| # | Due on | Problems |
|---|---|---|
| 1 | W 9/9 | Exercise §2.4. |
| — | R 9/10 | Retake (but do not hand in) quiz #1. |
| — | W 9/16 | Retake (but do not hand in) quiz #2. |
| 2 | R 9/17 | In R2 draw the spheres of radius 1 centered at the origin (0,0) with respect to: 1) the Euclidean metric; 2) the taxicab metric; 3) the square metric; and 4) the discrete metric. |
| 3 | M 9/21 | Retake (but do not hand in) quiz #3, and solve the following problems. A] Let (X,d) be an arbitrary metric space. Prove that for all distinct points x1 and x2 in X there exist positive real numbers ε1 and ε2 such that Bd(x1;ε1) and Bd(x2;ε2) are disjoint. B] Find a metric space and two balls in it such that the ball with smaller radius contains and is not equal to the ball with larger radius. |
| 4 | R 9/24 | Let (X,d) be an arbitrary metric space. Given any point a in X and any non-negative real number r, prove that { x∈X | d(a,x)≤r } is closed. |
| 5 | F 9/25 | Write down explicitly what it means for a function between metric spaces to be discontinuous. |
| 6 | M 10/5 | Retake (but do not hand in) quiz #4, and solve exercise §13.1: Let X be a topological space, and let A be a subset of X. Suppose that for each x∈A there is an open set U containing x such that U⊂A. Show that A is open in X. |
| 7 | R 10/8 | Prime time! |
| 8 | M 10/19 | Exercises §17.6, §17.7, and §17.8. |
| — | R 10/22 | Retake (but do not hand in) quiz #6. |
| 9 | W 11/4 | Let (X,d) be a metric space, let A be a subset of X, and let x be a point in X. Show that x is in the closure of A if and only if inf{d(x,a)|a∈A}=0. |
| — | M 11/9 | Riddle: consider a set S of disjoint figure-eight curves in the plane; can S be uncountable? |
| 10 | M 11/16 |
A] Show that the lower limit topology on R is
Hausdorff and first-countable, but not metrizable. (Hint: in
order to prove that it is not metrizable, show that it
is … but not …, and apply a result
discussed in class.) B] Show that any set of pairwise disjoint open subsets of a separable topological space is countable. C] Show that any discrete subspace of a second-countable topological space is countable. |
| — | R 11/12 | Retake (but do not hand in) quiz #7. |
| 11 | M 11/23 | In parts B] and C] below, the symbol R denotes
(as usual) the real numbers with the standard topology. A] Suppose that X and Y are topological spaces and that f: X → Y is a continuous function. Show that if X is compact then f(X) is compact. B] Suppose that C is a non-empty compact subspace of R. Show that C has a least element, i.e., that there exists c∈C such that for all x∈C we have c≤x. (Hint: argue by contradiction, and observe that { (x,∞) | x∈C } is an open cover of C if and only if C does not have a least element.) Is c unique? C] Suppose that X is a non-empty compact topological space and that f: X → R is a continuous function. Use parts A] and B] to show that there exists m∈X such that for all x∈X we have f(m)≤f(x). Is m unique? |
| 12 | M 11/30 | Study section §23 up to and including
theorem 23.5 (pages 148–150),
and solve exercises
§23.1, §23.2, §23.5, and §23.7
(recall that the symbol
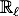 in §23.7 denotes
the real numbers with the lower limit topology). |
| 13 | M 12/7 | Exercises §24.3, §24.8(c), and §24.8(d). |
| — | M 12/7 | Retake (but do not hand in) quiz #9. |
![[Valid Atom 1.0]](valid-atom.png "Validate my Atom 1.0 feed")