Math 330: Introduction to Higher Math

(aka Number Systems, or simply Proofs)

Section 1, Spring 2009

Instructor

Marco Varisco, [email protected] [how to email a professor], math.binghamton.edu/marco/proofs/
Office: LN-2208A, Office Hours: MW 3:00–4:30 or by appointment.

Schedule

MWF 10:50–11:50 in SW-325 and R 10:05–11:05 in LN-G335.
N.B.: The Thursday meeting is not a discussion session.

You are expected to attend all class meetings. The maximum number of absences permitted to receive credit for this course is 5 (five). Excessive tardiness may count as absence. [University Bulletin]

Prerequisite

Math 222: Calculus II with a grade of C or better. [University Bulletin]

Description

“Careful discussion of the real numbers, the rational numbers and the integers, including a thorough study of induction and recursion. Countable and uncountable sets. The methodology of mathematics: basic logic, the use of quantifiers, equivalence relations, sets and functions. Methods of proof in mathematics. Training in how to discover and write proofs.” [University Bulletin]

Textbook

The Art of Proof: A Concrete Gateway to Mathematics, Matthias Beck and Ross Geoghegan, 2009.
This textbook is published by Binghamton University and is only available from local bookstores.

Grading & Examinations

50% – Homework, see below, and possibly some unannounced quizzes.
15% – Midterm Exam, scheduled for Thursday, March 12, 10:05–11:30 in LN-G335 (before the course withdrawal deadline, Friday, March 27).
15% – Project Assignment, due on Monday, May 4.
20% – Final Exam [solutions], scheduled for Monday, May 11, 11:00–1:00 in S1-149.

When calculating your course grade there is one more rule: if your homework score is an F then your course grade is an F; in this case I will ignore your midterm, project, and final exam scores.

Of course, you are expected to obey the Student Academic Honesty Code.

Homework

#	Due on	Problems
1	R 1/29	Prove propositions 1.7 & 1.10(ii).
2	M 2/02	Prove propositions 1.14, 1.15, & 1.20.
3	W 2/04	Prove propositions 1.16 & 1.19, and read chapter 2.
4	R 2/05	Reread chapter 2, and do projects 2.1 & 2.2.
5	M 2/09	Retake (but do not hand in) quiz #1, and do this.
6	R 2/12	Prove proposition 3.10(ii).
7	F 2/13	An integer n is called even if it is divisible by 2, i.e., if there exists an integer k such that n=2k. Question: Is 0 even? Why or why not? Prove the following statements: [A] If m and n are even then m+n and mn are even. [B] For any natural number n, n²+n is even. [C] For any natural number n, n is even or n+1 is even. [D] For any integer n, n is even or n+1 is even.
8	W 2/18	Prove propositions 3.17, 3.19, 3.20, & 3.23. An integer n is called odd if it is not even. Question: Is 1 odd? Why or why not? Prove the following statements: [E] For any integer n, either n is even or n+1 is even, but not both. [F] If n is an odd integer, then there exists an even integer m such that n=m-1. (You may use statements [A], [B], [C], & [D] from the previous assignment.)
9	W 2/25	Retake (but do not hand in) quiz #2, and prove that for any natural number k,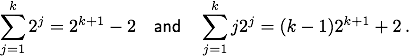 $\sum_{j=1}^k 2^j = 2^{k+1}-2, \sum_{j=1}^k j2^j = (k-1)2^{k+1}+2.$
10	W 3/04	Find a formula for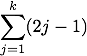 $\sum_{j=1}^k (2j-1)$ for any natural number k, and prove that your formula is correct.
11	R 3/05	Prove that for all natural numbers x and y, there exists a natural number n such that nx≥y.
12	W 3/11	Prove theorem 6.8. Prove that any non-empty, bounded above set of integers has a largest element.
13	F 3/27	Prime time!
14	M 3/30	Retake (but do not hand in) quiz #3, and prove propositions 10.6 & 10.12 (you may use proposition 10.11).
15	M 4/20	[1] Prove that the sequence (n-1)/n converges to 1. [2] Write down explicitly what it means for a sequence to be divergent. [3] Prove that any convergent sequence of real numbers is bounded above. [4] Prove that any non-decreasing and bounded above sequence of real numbers is convergent.
16	W 4/22	Retake (but do not hand in) quiz #5, and prove that the sequence x_n=(-1)ⁿ diverges.
17	M 4/27	Prove that the sequence defined recursively by x₁=2 and x_n+1=(x_n+6)/2 is convergent.

This syllabus is subject to change. All official announcements and assignments are given in class, and this web page may not be up to date.

Marco Varisco - May 12, 2009.